About the Scheil Calculator
The Scheil Calculator Allows You to Calculate:
Four Models for Scheil Solidification Simulations
Thermo-Calc includes four models for Scheil Solidification Simulations.
The Classic Scheil simulation is based on the well-known Scheil-Gulliver model and assumes zero diffusion in the solidified material.
A second model is available where one or more elements can be defined as “fast diffusers”.
Our third model uses diffusion data to calculate Back Diffusion in the Primary Phase.
A fourth model uses Solute Trapping in the primary phase for calculations that have a high solidification speed, such as Additive Manufacturing applications.
Tips and Tricks: Selecting the Right Model for Your Scheil Solidification Calculation

A Scheil Solidification Simulation of the Aluminum Alloy AA7075 comparing a Classic Scheil Simulation with two Scheil with Back Diffusion simulations and to experimental data.
Classic Scheil Model
The most well-known example of a non-equilibrium calculation is the Scheil-Gulliver solidification simulation, or Scheil simulation for short. This is the model used for our Classic Scheil simulations.
Classic Scheil Simulations Assume:
- Diffusion of all elements in the liquid phase is infinitely fast
- Diffusion of all elements in the solid phases is zero
- The liquid/solid interface is in thermodynamic equilibrium
This calculation procedure is equivalent to assuming that there is no diffusion in the solid phase and infinitely fast diffusion of all elements in the liquid phase. It has been shown to be a good approximation of the solidification of most alloys such as Ni-superalloys, Cu alloys, Al alloys, Mg alloys, and others. However, it does not work well for steels. For this reason, a variant of the Scheil simulation was developed and implemented in Thermo-Calc where one or more elements can be defined as “fast diffusers”.
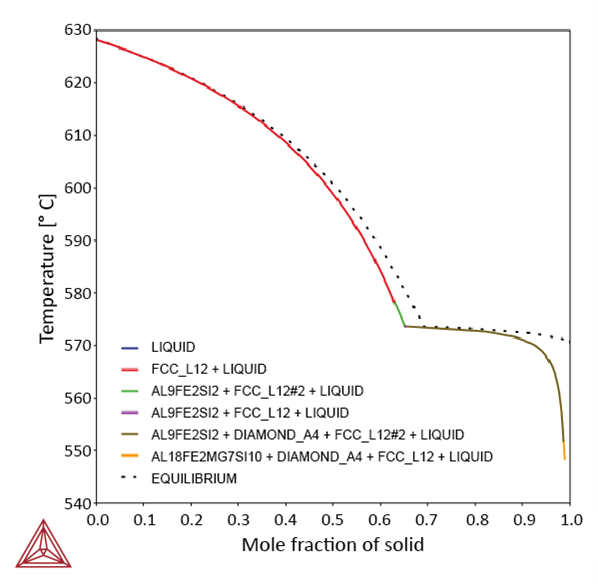
Classic Scheil Solidification Simulation of Aluminum Alloy 4043 compared to equilibrium.
Scheil with Fast Diffusers
Scheil with Fast Diffusers is a variant of the Classic Scheil simulation that was developed mainly for steel applications.
Scheil Simulation with Fast Diffusers Assume:
- Diffusion of all elements in the liquid phase is infinitely fast
- Diffusion of all elements in the solid phases except the ones defined as “fast diffusers” is zero
- Diffusion of the elements defined as “fast diffusers” is infinitely fast in the solid phase
- The liquid/solid interface is in thermodynamic equilibrium
Carbon is one of the most important alloying elements in steels. It dissolves interstitially and, as a result, has very fast diffusion rates. The assumption of no diffusion in the solid phase during solidification is thus not correct for carbon at most industrial or lab-scale solidification rates. Scheil with Fast Diffusers allows one or more elements to be defined as “fast diffusers,” correcting for the problems addressed above. Typically, C is defined as a fast diffuser, but also other elements such as N, O, or others can be defined.

A Scheil Solidification Simulation for a steel with Fe0.8%Mn0.7%Si0.03%P0.4%C comparing a classic Scheil Simulation (green line) to Scheil with Fast Diffusers (brown line) and equilibrium (dotted line). As the plot shows, Scheil with Fast Diffusers is closer to equilibrium as the solidification progresses.
Scheil with Back Diffusion
A more advanced Scheil model, this model uses diffusion data from a mobility database to calculate back diffusion in the primary phase.
Scheil with Back Diffusion Assumes:
- Diffusion of all elements in the liquid phase is infinitely fast
- Diffusion of all elements in the primary solid phase is quantitatively calculated using mobility data, a cooling rate, and a domain size (typically this will be the secondary arm spacing)
- The liquid/solid interface is in thermodynamic equilibrium
As with the Scheil-Gulliver model, this model assumes infinitely fast diffusion in the liquid material, but it allows for limited diffusion in the primary phase of the solid material. Using diffusion data from a mobility database, it quantitatively takes into account the real back diffusion of all elements in the primary solid phase (typically the FCC or BCC phase). This model also allows setting selected components to be “fast diffusers,” and these are treated as if there is infinite diffusivity in the solid phases.
Scheil with Back Diffusion requires the use of a mobility database as it is using diffusion data to complete the calculation.

A Scheil Solidification Simulation with Back Diffusion of an Al-Cu-Si alloy comparing a cooling rate of 10 K/s (left line) to a cooling rate of 0.005 K/S (right line). As the plot shows, the lower cooling rate is closer to equilibrium as the solidification progresses.
Scheil with Solute Trapping
This model uses Solute Trapping in the primary phase for calculations that have a high solidification speed, such as Additive Manufacturing applications.
Scheil with Solute Trapping Assumes:
- Only one primary solid phase forms dendrite, NOT necessarily the first solid phase
- Solute trapping in primary solid phase only. Other solid phases have equilibrium compositions following the classic Scheil model
- Amounts of solid phases are dependent on solute trapping and solidification speed
- Dynamic liquidus for primary solid phase is dependent on solute trapping and solidification speed
- Dynamic solidus is calculated as complete solidification
The Scheil with Solute Trapping model is based on the main assumption that the primary phase is the only dendrite forming phase within which solute trapping is induced by high solidification speed. The resulting solute trapping also affects composition and amount of other solid phases.
Learn more by reading a presentation by the developers of the model.

A Scheil Solidification Simulation for an Al-Si-Mg alloy using the Solute Trapping model compared to a Classic Scheil Solidification Simulation and equilibrium. As the plot shows, the solute trapping model is closer to equilibrium as the solidification progresses.

How to Select the Right Model for Your Scheil Calculation
Not sure which Scheil Module to use? We have a blog post that just might help. This blog post discusses the different model configurations included in the calculator to give you guidance on when to use which model configuration for your Scheil solidification calculations.

WEBINAR
Solidification Modelling With CALPHAD:
Process Applications of Equilibrium and Non-equilibrium Models and When to Use Them
This presentation outlines the various CALPHAD-based solidification models, and discuss when each should be applied using industry focused case studies.

Export to Additive Manufacturing Module or External FEM Simulation Software
The Scheil Module can be used to generate the materials property data needed for simulations in the Additive Manufacturing Module. The two modules are seamlessly linked in the software, so data is automatically transferred from Scheil to the Additive Manufacturing Module. A license for the Additive Manufacturing Module is required.
Additionally, the materials data can be tabulated and saved on file for export to external FEM simulation software.
Learn More about Scheil Solidification Simulations
A collection of videos demonstrating some of the capabilities of the Scheil Solidification Calculator.
Development of Non-Equilibrium Thermodynamic Tools for Additive Manufacturing
Modelling of additive manufacturability of nickel-based superalloys for laser powder bed fusion